Series on Blogging with LaTeX
This is the 2nd post in the series. Previous one:
This series shows my first experiences with using the mathematical expressions handling tools provided by WordPress for blogging. They use a version of the LaTeX syntax.
Many of the examples shown here were adapted from the Wikipedia article Displaying a formula, which is actually about formulas in Math Markup.
.
Accents – Diacritics
Examples on how to put accents in mathematical expressions:
\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}
\check{a} \bar{a} \ddot{a} \dot{a}
x’, y”
.
Superscript and subscript
How to display subscripts and superscripts, indexes and exponents:
Subscripts:
- a_i gives
- b_{ij} gives
- C_{m,n} gives
- \delta_{j+k} gives
Superscripts:
- x^y gives
- a^{j2\pi} gives
- x^2_3 gives
- C^k_{\mu,\nu} gives
Composition with preceding indexes: {}_1^2 \Psi_3^4 gives
.
Underlines, overlines and stackings
Includes vectors
\hat a \ \bar b \ \vec c
\overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f}
\overline{g h i} \ \underline{j k l}
\overbrace{ 1+2+\cdots+100 }^{5050}
\underbrace{ a+b+\cdots+z }_{26}
A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C
\overset{\alpha}{\omega} \underset{\mu}{\nu} \overset{\beta}{\underset{\Delta}{\tau}} \stackrel{\zeta}{\eta}
.
Sets
Sets operations and related symbols.
\in \ni \notin \varnothing \complement
\subset \subseteq \subsetneq \supset \supseteq \supsetneq
\cap \bigcap \cup \bigcup
\ell \mho \Finv \Re \Im \wp
Others – examples using the calligraphic font (\cal) and the Greek font for designating sets:
{\cal A} \setminus {\cal B} gives
\Omega \smallsetminus \omega gives
.
Logic
Logical operators and relations:
\forall \exists \nexists \bar{A} \mid
\And \wedge \vee \neg \to \gets \iff
\bigwedge \bigvee \diamond \lozenge
\vdash \Vdash \vDash \Vvdash \models \dashv
Examples:
- \forall p,q \, \exists q \mid \bar{q} \to p gives
- \bigwedge _{x \in A} gives
- \bigwedge \limits _{x \notin A} gives
- \bar{A \vee B} = \bar{A} \wedge \bar{B} gives
- A \iff B = A \to B \wedge A \gets B gives
- \bigcap \limits _{i=1}^n \bigcup \limits _{j=1}^n {\cal B}_{i,j} gives
Obs – the statement \limits shown in the examples above puts the indexes exactly above and / or below the symbol. In the first example, \, is used to put an extra space. .
Operators
Several types of operators:
+ \oplus \bigoplus \pm \mp –
\times \otimes \bigotimes \cdot \circ \bullet \bigodot
\star * / \div \frac{1}{2}
\sqrt{2} \sqrt[n]{x}
\nabla \partial x \dot x \ddot y
Examples:
- \rho = \sqrt{x^2 + y^2} gives
- \nabla \phi (x,y) = \frac{\partial \phi}{\partial x} + \frac{\partial \phi}{\partial y} gives
- \nabla^2 \phi (x,y) = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} gives
- \frac{\partial^2 \phi}{\partial x \partial y} = \frac{\partial^2 \phi}{\partial y \partial x} gives
.
Relations and definitions
To specify relations, mappings and definitions
\sim \approx \simeq \cong \dot =
< > \le \ge \ll \gg
\lessgtr \lesseqgtr \lesseqqgtr
\equiv \not\equiv \ne \propto
\mapsto \longmapsto
.
Geometric
Geometric symbols
\circ \bigcirc \Diamond \Box \triangle
\vartriangle \triangledown \triangleleft \triangleright \vartriangleright \vartriangleleft
\angle \sphericalangle \measuredangle 45^\circ
\perp \mid \nmid \| \asymp \parallel
.
Arrows
Some more frequent types of arrows (there are many more – see in Wikipedia article)
\leftarrow \rightarrow \leftrightarrow \Leftarrow \Rightarrow \Leftrightarrow
\leftarrow \gets \rightarrow \to \not\to \leftrightarrow \longleftarrow \longrightarrow
\rightleftharpoons \leftleftarrows \leftrightarrows \Lleftarrow \leftarrowtail
\uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow
.
Special symbols
Some special symbols. There are many more in Wikipedia article
\S \P \% \dagger \ddagger \ldots \cdots
\smile \frown \wr \triangleleft \triangleright \infty \bot \top
\imath \hbar \jmath \surd \ast \amalg \therefore \backepsilon \sharp
.
Summations, Integrals and Products
Several cases, including limits, sequences and series. Notice in the examples below that when you want to put the limits with the same vertical alignment of the math symbol, you must use the \limits declaration. Otherwise, the limits will be put ahead of the symbol.
\lim \limits_{n \to \infty}x_n
\lim _{n \to \infty}x_n
\sum_{k=1}^N k^2
\sum \limits_{k=1}^N k^2
\prod_{i=1}^N x_i
\prod \limits_{i=1}^N x_i
\coprod_{i=1}^N x_i
\coprod \limits_{i=1}^N x_i
\int_{-N}^{N} e^x\, dx
\int \limits_{-N}^{N} e^x\, dx
\iint_{D}^{W} \, dx\,dy
\iiint_{E}^{V} \, dx\,dy\,dz
\iiiint_{F}^{U} \, dx\,dy\,dz\,dt
\oint_{C} x^3\, dx + 4y^2\, dy
Obs – the declaration \, in the above integrals puts extra spaces between consecutive letters. See more about alignement on this post : LaTeX – Fine-tunning and some extras.
.
Binomials
Binomials only. For matrices, see next post.
\binom{n}{p} = \frac{n!}{p!(n-p)!}

48 comments
Comments feed for this article
March 22, 2008 at 9:49 am
Math Resources Blog » LaTeX - Use of math symbols and equations
[…] Slava Pestov: […]
March 22, 2008 at 12:11 pm
JoeV
Can you please host this information in pdf format?
March 22, 2008 at 4:20 pm
machinehuman
Nice post João! LaTeX is really nifty.
March 22, 2008 at 5:23 pm
Joao Kogler
Hi JoeV,
I’m still trying to figure out how practical could it be to leave this information only as a post or as a page. However, sooner I’ll make a pdf version joining all my recent posts in this subject. Check my homepage in about two weeks. I’m doing a large scale maintenance in my website by the moment.
March 23, 2008 at 3:37 am
jacob
Why not use \iff, \implies, etc., in favor of the longer “\blahblaharrow” forms?
March 23, 2008 at 3:38 am
jacob
* instead of, not in favor of
March 23, 2008 at 5:28 am
Joao Kogler
Yeah, Jacob, u’re right ! I was almost forgetting… too many blahblaharrows..
I’ll take care of them soon.
Thanks !
November 6, 2008 at 3:17 pm
Mauro
João, do you know what is the convention when representing the complement of a set? The obvious choice would be to use \bar, but it looks too small on capital letters like $\bar{\mathcal{M}}_{s_j}^l$ , for instance. $\overline{\mathcal{M}}_{s_j}^l$ looks awfull as well (and apparently it’s not its intended use).
Obrigado. Bom trabalho.
November 7, 2008 at 5:43 pm
Mauro
Solved, I guess it is supposed to look like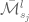 . Thanks anyway.
. Thanks anyway.
November 9, 2008 at 3:13 pm
Joao Kogler
Hi Mauro, actually the \overline is the recommended for the complement of a set, given that it provides scalability to wider expressions. So, it should display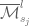 . The expression would show a better visual result if a space would be used before the exponent, like: $\overline{\mathcal{M}}_{s_j}^{\;l} $, that renders
. The expression would show a better visual result if a space would be used before the exponent, like: $\overline{\mathcal{M}}_{s_j}^{\;l} $, that renders 
February 19, 2009 at 1:14 am
R Todd Nelson
I’m trying to find out how to write several symbols from Geometry, namely the symbols for “line AB”, “arc AB”, and “parallelogram ABCD”. Any help would be greatly appreciated!
February 19, 2009 at 10:32 pm
Joao Kogler
Hi Todd,
I’d use \stackrel{\frown}{AB} for arc AB, that is quite usual. However, I don’t know any usual simbols for “line AB”or “parallelogram ABCD”. You are free to create your own symbols. You’ll find in my posts several examples of how you could use LaTeX rules to build them. I’ll show some ideas:
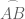
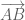
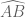
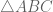
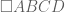
segment AB: \overline{AB}
arc AB: \stackrel{\frown}{AB}
vector AB: \overrightarrow {AB}
angle AB: \widehat{AB}
triangle ABC: \triangle ABC
square ABCD: \Box ABCD
Maybe you’d consider using \diamond for the parallelogram, however it is not usual but could be used to avoid many repetitions of the word in a text.
April 28, 2009 at 3:57 am
JR
The package yhmath gives the command \wideparen, so write \usepackage{yhmath} in the preamble in order to use this command.
\begin{document}
$\wideparen{AB}$
\end{document}
Good Luck!!
May 15, 2009 at 4:10 pm
Hello world! « xcellenc
[…] Hello world! By alanzed Tonight I’ve made the switch-over from blogging on my localhost computer to onto the wordpress.com site. Hello world indeed. I’ve got to spend a bit of time fixing up older posts so the LaTeX comes up correctly, so I’ll be in editing mode for a while. Fortunately, there is lots of help WordPress + LaTeX. Kogler has a posting with a nice summary. […]
October 1, 2009 at 1:33 pm
Chris Tompsett
An useful addition would be the large dot ({\hspace*{2 pt} \text{\huge {.}} \hspace*{2 pt}}) to support the use of Quine/Church notation.
January 11, 2010 at 2:33 am
Guillermo Bautista
Hi. I also have created a latex tutorial here:
http://math4allages.wordpress.com/view-posts-by-topics/
http://math4allages.wordpress.com/2009/12/06/latex-tutorial/
http://math4allages.wordpress.com/2009/12/09/latex-basic-commands/
you may want to check it out.
January 20, 2010 at 2:33 pm
Joao Kogler
Nice blogs, I’ll recommend them to my students. Feel free to link my posts on LaTeX in your tutorials.
Joao
January 21, 2010 at 1:16 am
Guillermo Bautista
Yes, I am going to link this post.
January 21, 2010 at 1:20 am
Latex Tutorial: Commonly Used Latex Commands « Mathematics and Multimedia
[…] Mr. Kogler has also a latex tutorial for for advanced users here. […]
July 25, 2010 at 10:16 pm
Latex : Derivatives limits sums and integrals « Live
[…] July 25, 2010 in Latex, Learn how to use wordpress reference link 1 reference link 2 […]
October 6, 2010 at 3:25 pm
gasstationwithoutpumps
For help with LaTeX, there are a lot of great web sites already. Blogging does add an extra wrinkle, in that WordPress does not provide any error messages from the LaTeX compiler, so it can be difficult to debug your typos. If you are doing complex things on a blog, it may be better to create a LaTeX document first, debug the expressions there, then cut and paste it into the blog.
I chose WordPress as my blogging platform because of its decent support for LaTeX. (See my post http://gasstationwithoutpumps.wordpress.com/2010/07/08/latex-on-wordpress/ )
March 7, 2011 at 12:39 am
数学公式编辑参考1 | 师域 www.09-10.com
[…] LaTeX – Use of math symbols and equations « Machine Intelligence ? […]
March 30, 2011 at 4:40 am
dr prem raj pushpakaran
liked very much
June 25, 2011 at 9:40 am
LaTeX – Multiline equations, systems and matrices « Robert's World
[…] Use of mathematical symbols in formulas and equations […]
August 25, 2011 at 6:08 pm
Transformada inversa de Laplace (caso 2) | Experimentos do Dia a Dia
[…] Outros exemplos de Latex no WordPress:https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ acesso em 25/08/2011 as 14h02 GMT -04h00. Like this:LikeBe the first to like this […]
August 26, 2011 at 3:36 am
Alguns Exemplos de uso do LaTex no Wordpress | Experimentos do Dia a Dia
[…] [1] https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ […]
August 26, 2011 at 4:26 pm
Alguns Exemplos de uso do LaTex no Wordpress « Zettadata
[…] [1] https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ […]
August 26, 2011 at 4:30 pm
Transformada inversa de Laplace (caso 2) « Zettadata
[…] Outros exemplos de Latex no WordPress:https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ acesso em 25/08/2011 as 14h02 GMT -04h00. Share this:TwitterFacebookLike this:LikeBe the first to […]
May 6, 2012 at 7:15 pm
zhunxu2011
Reblogged this on zhunxu and commented:
Thanks for Joao Kogler’s help. I’m learning hwo to type mathematical expressions in WordPress. This is his article.
September 2, 2012 at 2:18 pm
WANGARI ISAAC MWANGI
Thank you very much for your valuable mathematical symbols.
April 7, 2013 at 7:22 pm
Raghwendra kumar
thanks a lot ,this is really very nice
April 19, 2013 at 9:33 pm
Theresa
I used to be suggested this web site via my cousin. I’m now not certain whether this post is written by means of him as no one else realize such detailed about my problem. You are incredible! Thank you!
May 13, 2013 at 1:28 pm
Joao Kogler
Thanks for everyone who expressed their experience with this post. I actually had it written in 2008 as an exercise to get more experience with WordPress LaTeX before I get into more serious posts and to rest as a reference for future use. I had never expected that it could have such a big interest (in the day after I’d posted it I checked the stats and there were over 3000 accesses ! ). Nevertheless, I’ve been using all this in my other WordPress blog Videlicet, directed to my students (http://jkogler.wordpress.com/). I’m still looking for an opportunity to get back to this blog, although the stream is taking me the other way 🙂
June 4, 2013 at 8:36 am
physicslight
good job !
November 17, 2013 at 5:17 am
Latex | Vic's World
[…] https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ […]
February 3, 2014 at 2:26 pm
LaTeX Code in WordPress : Write Equations in Posts with Beautiful Math
[…] can find more information about amsmath package syntaxes at https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ […]
March 12, 2014 at 5:00 am
Badil masih
Goog work my help.
September 18, 2014 at 1:35 pm
Smithe2
Hello.This post was extremely motivating, especially because I was browsing for thoughts on this subject last Thursday. kgeddckgbkgedgda
December 4, 2014 at 12:56 am
herminiohon
Thank you very much.
April 21, 2015 at 8:21 am
Entering LaTeX Maths Symbols | GoConqr
[…] guide here or if you’re feeling like a pro you can read more in-depth guides on Wikibooks and Kogler. If you still can’t find what you’re looking for then just ask us and we’ll try […]
September 12, 2015 at 5:56 pm
Daniel
Grateful for help me. The informations were very important for my job!
January 26, 2016 at 3:27 pm
Basic Multivariate Statistics and Principal Component Analysis (PCA) – 我們的基因體時代
[…] LaTeX – Use of math symbols and equations. […]
June 16, 2016 at 2:03 am
Anuj Gupta
Great post. How do you write cases in word press ? this gives error :
Any suggestions ?
September 4, 2016 at 4:12 pm
Geometría en latex – galoisian
[…] https://kogler.wordpress.com/2008/03/21/latex-use-of-math-symbols-formulas-and-equations/ […]
November 6, 2016 at 12:30 am
Njongwe James
Thanks so much for the information. I am a beginner in this LaTex field and this piece has taken me to a very high level.once more, am so so grateful.
March 30, 2017 at 3:37 pm
How I build this blog on WordPress (Update time to time) – 饱蠹阁baoduge
[…] Document: LaTeX – Use of math symbols and equations LaTeX – Use of math symbols and equations […]
December 26, 2017 at 2:30 pm
Latex symbol – MathBlog
[…] 還有這一個:LaTeX – Use of math symbols and equations […]
March 19, 2018 at 8:26 pm
Alex
THE BEST CHEATSHEETS